Mathematical gradient operator in certain coordinate systems
This is a list of some vector calculus formulae for working with common curvilinear coordinate systems .
Notes This article uses the standard notation ISO 80000-2 , which supersedes ISO 31-11 , for spherical coordinates (other sources may reverse the definitions of θ and φ ):The polar angle is denoted by θ ∈ [ 0 , π ] {\displaystyle \theta \in [0,\pi ]} z -axis and the radial vector connecting the origin to the point in question. The azimuthal angle is denoted by φ ∈ [ 0 , 2 π ] {\displaystyle \varphi \in [0,2\pi ]} x -axis and the projection of the radial vector onto the xy -plane. The function atan2 (y , x )arctan (y /x )domain and image . The classical arctan function has an image of (−π/2, +π/2) , whereas atan2 is defined to have an image of (−π, π] .
Coordinate conversions Note that the operation arctan ( A B ) {\displaystyle \arctan \left({\frac {A}{B}}\right)} atan2 .
Unit vector conversions
^α θ {\displaystyle \theta } φ {\displaystyle \varphi } θ {\displaystyle \theta } φ {\displaystyle \varphi } θ {\displaystyle \theta } φ {\displaystyle \varphi } ^β ∂ i A ⊗ e i {\displaystyle \partial _{i}\mathbf {A} \otimes \mathbf {e} _{i}} e i ⊗ ∂ i A {\displaystyle \mathbf {e} _{i}\otimes \partial _{i}\mathbf {A} } ^γ e i ⋅ ∂ i T {\displaystyle \mathbf {e} _{i}\cdot \partial _{i}\mathbf {T} } ∂ i T ⋅ e i {\displaystyle \partial _{i}\mathbf {T} \cdot \mathbf {e} _{i}}
Calculation rules div grad f ≡ ∇ ⋅ ∇ f ≡ ∇ 2 f {\displaystyle \operatorname {div} \,\operatorname {grad} f\equiv \nabla \cdot \nabla f\equiv \nabla ^{2}f} curl grad f ≡ ∇ × ∇ f = 0 {\displaystyle \operatorname {curl} \,\operatorname {grad} f\equiv \nabla \times \nabla f=\mathbf {0} } div curl A ≡ ∇ ⋅ ( ∇ × A ) = 0 {\displaystyle \operatorname {div} \,\operatorname {curl} \mathbf {A} \equiv \nabla \cdot (\nabla \times \mathbf {A} )=0} curl curl A ≡ ∇ × ( ∇ × A ) = ∇ ( ∇ ⋅ A ) − ∇ 2 A {\displaystyle \operatorname {curl} \,\operatorname {curl} \mathbf {A} \equiv \nabla \times (\nabla \times \mathbf {A} )=\nabla (\nabla \cdot \mathbf {A} )-\nabla ^{2}\mathbf {A} } Lagrange's formula for del)∇ 2 ( f g ) = f ∇ 2 g + 2 ∇ f ⋅ ∇ g + g ∇ 2 f {\displaystyle \nabla ^{2}(fg)=f\nabla ^{2}g+2\nabla f\cdot \nabla g+g\nabla ^{2}f} ∇ 2 ( P ⋅ Q ) = Q ⋅ ∇ 2 P − P ⋅ ∇ 2 Q + 2 ∇ ⋅ [ ( P ⋅ ∇ ) Q + P × ∇ × Q ] {\displaystyle \nabla ^{2}\left(\mathbf {P} \cdot \mathbf {Q} \right)=\mathbf {Q} \cdot \nabla ^{2}\mathbf {P} -\mathbf {P} \cdot \nabla ^{2}\mathbf {Q} +2\nabla \cdot \left[\left(\mathbf {P} \cdot \nabla \right)\mathbf {Q} +\mathbf {P} \times \nabla \times \mathbf {Q} \right]\quad }
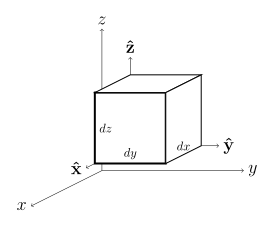
Cartesian derivation
div A = lim V → 0 ∬ ∂ V A ⋅ d S ∭ V d V = A x ( x + d x ) d y d z − A x ( x ) d y d z + A y ( y + d y ) d x d z − A y ( y ) d x d z + A z ( z + d z ) d x d y − A z ( z ) d x d y d x d y d z = ∂ A x ∂ x + ∂ A y ∂ y + ∂ A z ∂ z {\displaystyle {\begin{aligned}\operatorname {div} \mathbf {A} =\lim _{V\to 0}{\frac {\iint _{\partial V}\mathbf {A} \cdot d\mathbf {S} }{\iiint _{V}dV}}&={\frac {A_{x}(x+dx)\,dy\,dz-A_{x}(x)\,dy\,dz+A_{y}(y+dy)\,dx\,dz-A_{y}(y)\,dx\,dz+A_{z}(z+dz)\,dx\,dy-A_{z}(z)\,dx\,dy}{dx\,dy\,dz}}\\&={\frac {\partial A_{x}}{\partial x}}+{\frac {\partial A_{y}}{\partial y}}+{\frac {\partial A_{z}}{\partial z}}\end{aligned}}}
( curl A ) x = lim S ⊥ x ^ → 0 ∫ ∂ S A ⋅ d ℓ ∬ S d S = A z ( y + d y ) d z − A z ( y ) d z + A y ( z ) d y − A y ( z + d z ) d y d y d z = ∂ A z ∂ y − ∂ A y ∂ z {\displaystyle {\begin{aligned}(\operatorname {curl} \mathbf {A} )_{x}=\lim _{S^{\perp \mathbf {\hat {x}} }\to 0}{\frac {\int _{\partial S}\mathbf {A} \cdot d\mathbf {\ell } }{\iint _{S}dS}}&={\frac {A_{z}(y+dy)\,dz-A_{z}(y)\,dz+A_{y}(z)\,dy-A_{y}(z+dz)\,dy}{dy\,dz}}\\&={\frac {\partial A_{z}}{\partial y}}-{\frac {\partial A_{y}}{\partial z}}\end{aligned}}}
The expressions for ( curl A ) y {\displaystyle (\operatorname {curl} \mathbf {A} )_{y}} ( curl A ) z {\displaystyle (\operatorname {curl} \mathbf {A} )_{z}}
Cylindrical derivation
div A = lim V → 0 ∬ ∂ V A ⋅ d S ∭ V d V = A ρ ( ρ + d ρ ) ( ρ + d ρ ) d ϕ d z − A ρ ( ρ ) ρ d ϕ d z + A ϕ ( ϕ + d ϕ ) d ρ d z − A ϕ ( ϕ ) d ρ d z + A z ( z + d z ) d ρ ( ρ + d ρ / 2 ) d ϕ − A z ( z ) d ρ ( ρ + d ρ / 2 ) d ϕ ρ d ϕ d ρ d z = 1 ρ ∂ ( ρ A ρ ) ∂ ρ + 1 ρ ∂ A ϕ ∂ ϕ + ∂ A z ∂ z {\displaystyle {\begin{aligned}\operatorname {div} \mathbf {A} &=\lim _{V\to 0}{\frac {\iint _{\partial V}\mathbf {A} \cdot d\mathbf {S} }{\iiint _{V}dV}}\\&={\frac {A_{\rho }(\rho +d\rho )(\rho +d\rho )\,d\phi \,dz-A_{\rho }(\rho )\rho \,d\phi \,dz+A_{\phi }(\phi +d\phi )\,d\rho \,dz-A_{\phi }(\phi )\,d\rho \,dz+A_{z}(z+dz)\,d\rho \,(\rho +d\rho /2)\,d\phi -A_{z}(z)\,d\rho (\rho +d\rho /2)\,d\phi }{\rho \,d\phi \,d\rho \,dz}}\\&={\frac {1}{\rho }}{\frac {\partial (\rho A_{\rho })}{\partial \rho }}+{\frac {1}{\rho }}{\frac {\partial A_{\phi }}{\partial \phi }}+{\frac {\partial A_{z}}{\partial z}}\end{aligned}}}
( curl A ) ρ = lim S ⊥ ρ ^ → 0 ∫ ∂ S A ⋅ d ℓ ∬ S d S = A ϕ ( z ) ( ρ + d ρ ) d ϕ − A ϕ ( z + d z ) ( ρ + d ρ ) d ϕ + A z ( ϕ + d ϕ ) d z − A z ( ϕ ) d z ( ρ + d ρ ) d ϕ d z = − ∂ A ϕ ∂ z + 1 ρ ∂ A z ∂ ϕ {\displaystyle {\begin{aligned}(\operatorname {curl} \mathbf {A} )_{\rho }&=\lim _{S^{\perp {\hat {\boldsymbol {\rho }}}}\to 0}{\frac {\int _{\partial S}\mathbf {A} \cdot d{\boldsymbol {\ell }}}{\iint _{S}dS}}\\[1ex]&={\frac {A_{\phi }(z)\left(\rho +d\rho \right)\,d\phi -A_{\phi }(z+dz)\left(\rho +d\rho \right)\,d\phi +A_{z}(\phi +d\phi )\,dz-A_{z}(\phi )\,dz}{\left(\rho +d\rho \right)\,d\phi \,dz}}\\[1ex]&=-{\frac {\partial A_{\phi }}{\partial z}}+{\frac {1}{\rho }}{\frac {\partial A_{z}}{\partial \phi }}\end{aligned}}}
( curl A ) ϕ = lim S ⊥ ϕ ^ → 0 ∫ ∂ S A ⋅ d ℓ ∬ S d S = A z ( ρ ) d z − A z ( ρ + d ρ ) d z + A ρ ( z + d z ) d ρ − A ρ ( z ) d ρ d ρ d z = − ∂ A z ∂ ρ + ∂ A ρ ∂ z {\displaystyle {\begin{aligned}(\operatorname {curl} \mathbf {A} )_{\phi }&=\lim _{S^{\perp {\boldsymbol {\hat {\phi }}}}\to 0}{\frac {\int _{\partial S}\mathbf {A} \cdot d{\boldsymbol {\ell }}}{\iint _{S}dS}}\\&={\frac {A_{z}(\rho )\,dz-A_{z}(\rho +d\rho )\,dz+A_{\rho }(z+dz)\,d\rho -A_{\rho }(z)\,d\rho }{d\rho \,dz}}\\&=-{\frac {\partial A_{z}}{\partial \rho }}+{\frac {\partial A_{\rho }}{\partial z}}\end{aligned}}}
( curl A ) z = lim S ⊥ z ^ → 0 ∫ ∂ S A ⋅ d ℓ ∬ S d S = A ρ ( ϕ ) d ρ − A ρ ( ϕ + d ϕ ) d ρ + A ϕ ( ρ + d ρ ) ( ρ + d ρ ) d ϕ − A ϕ ( ρ ) ρ d ϕ ρ d ρ d ϕ = − 1 ρ ∂ A ρ ∂ ϕ + 1 ρ ∂ ( ρ A ϕ ) ∂ ρ {\displaystyle {\begin{aligned}(\operatorname {curl} \mathbf {A} )_{z}&=\lim _{S^{\perp {\hat {\boldsymbol {z}}}}\to 0}{\frac {\int _{\partial S}\mathbf {A} \cdot d\mathbf {\ell } }{\iint _{S}dS}}\\[1ex]&={\frac {A_{\rho }(\phi )\,d\rho -A_{\rho }(\phi +d\phi )\,d\rho +A_{\phi }(\rho +d\rho )(\rho +d\rho )\,d\phi -A_{\phi }(\rho )\rho \,d\phi }{\rho \,d\rho \,d\phi }}\\[1ex]&=-{\frac {1}{\rho }}{\frac {\partial A_{\rho }}{\partial \phi }}+{\frac {1}{\rho }}{\frac {\partial (\rho A_{\phi })}{\partial \rho }}\end{aligned}}}
curl A = ( curl A ) ρ ρ ^ + ( curl A ) ϕ ϕ ^ + ( curl A ) z z ^ = ( 1 ρ ∂ A z ∂ ϕ − ∂ A ϕ ∂ z ) ρ ^ + ( ∂ A ρ ∂ z − ∂ A z ∂ ρ ) ϕ ^ + 1 ρ ( ∂ ( ρ A ϕ ) ∂ ρ − ∂ A ρ ∂ ϕ ) z ^ {\displaystyle {\begin{aligned}\operatorname {curl} \mathbf {A} &=(\operatorname {curl} \mathbf {A} )_{\rho }{\hat {\boldsymbol {\rho }}}+(\operatorname {curl} \mathbf {A} )_{\phi }{\hat {\boldsymbol {\phi }}}+(\operatorname {curl} \mathbf {A} )_{z}{\hat {\boldsymbol {z}}}\\[1ex]&=\left({\frac {1}{\rho }}{\frac {\partial A_{z}}{\partial \phi }}-{\frac {\partial A_{\phi }}{\partial z}}\right){\hat {\boldsymbol {\rho }}}+\left({\frac {\partial A_{\rho }}{\partial z}}-{\frac {\partial A_{z}}{\partial \rho }}\right){\hat {\boldsymbol {\phi }}}+{\frac {1}{\rho }}\left({\frac {\partial (\rho A_{\phi })}{\partial \rho }}-{\frac {\partial A_{\rho }}{\partial \phi }}\right){\hat {\boldsymbol {z}}}\end{aligned}}}
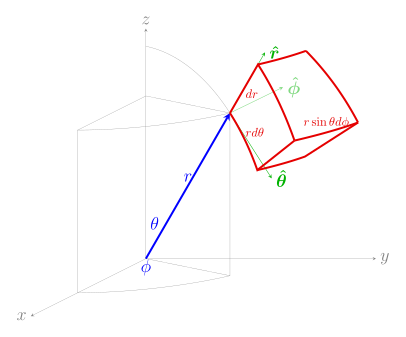
Spherical derivation div A = lim V → 0 ∬ ∂ V A ⋅ d S ∭ V d V = A r ( r + d r ) ( r + d r ) d θ ( r + d r ) sin θ d ϕ − A r ( r ) r d θ r sin θ d ϕ + A θ ( θ + d θ ) sin ( θ + d θ ) r d r d ϕ − A θ ( θ ) sin ( θ ) r d r d ϕ + A ϕ ( ϕ + d ϕ ) r d r d θ − A ϕ ( ϕ ) r d r d θ d r r d θ r sin θ d ϕ = 1 r 2 ∂ ( r 2 A r ) ∂ r + 1 r sin θ ∂ ( A θ sin θ ) ∂ θ + 1 r sin θ ∂ A ϕ ∂ ϕ {\displaystyle {\begin{aligned}\operatorname {div} \mathbf {A} &=\lim _{V\to 0}{\frac {\iint _{\partial V}\mathbf {A} \cdot d\mathbf {S} }{\iiint _{V}dV}}\\&={\frac {A_{r}(r+dr)(r+dr)\,d\theta \,(r+dr)\sin \theta \,d\phi -A_{r}(r)r\,d\theta \,r\sin \theta \,d\phi +A_{\theta }(\theta +d\theta )\sin(\theta +d\theta )r\,dr\,d\phi -A_{\theta }(\theta )\sin(\theta )r\,dr\,d\phi +A_{\phi }(\phi +d\phi )r\,dr\,d\theta -A_{\phi }(\phi )r\,dr\,d\theta }{dr\,r\,d\theta \,r\sin \theta \,d\phi }}\\&={\frac {1}{r^{2}}}{\frac {\partial (r^{2}A_{r})}{\partial r}}+{\frac {1}{r\sin \theta }}{\frac {\partial (A_{\theta }\sin \theta )}{\partial \theta }}+{\frac {1}{r\sin \theta }}{\frac {\partial A_{\phi }}{\partial \phi }}\end{aligned}}}
( curl A ) r = lim S ⊥ r ^ → 0 ∫ ∂ S A ⋅ d ℓ ∬ S d S = A θ ( ϕ ) r d θ + A ϕ ( θ + d θ ) r sin ( θ + d θ ) d ϕ − A θ ( ϕ + d ϕ ) r d θ − A ϕ ( θ ) r sin ( θ ) d ϕ r d θ r sin θ d ϕ = 1 r sin θ ∂ ( A ϕ sin θ ) ∂ θ − 1 r sin θ ∂ A θ ∂ ϕ {\displaystyle {\begin{aligned}(\operatorname {curl} \mathbf {A} )_{r}=\lim _{S^{\perp {\boldsymbol {\hat {r}}}}\to 0}{\frac {\int _{\partial S}\mathbf {A} \cdot d\mathbf {\ell } }{\iint _{S}dS}}&={\frac {A_{\theta }(\phi )r\,d\theta +A_{\phi }(\theta +d\theta )r\sin(\theta +d\theta )\,d\phi -A_{\theta }(\phi +d\phi )r\,d\theta -A_{\phi }(\theta )r\sin(\theta )\,d\phi }{r\,d\theta \,r\sin \theta \,d\phi }}\\&={\frac {1}{r\sin \theta }}{\frac {\partial (A_{\phi }\sin \theta )}{\partial \theta }}-{\frac {1}{r\sin \theta }}{\frac {\partial A_{\theta }}{\partial \phi }}\end{aligned}}}
( curl A ) θ = lim S ⊥ θ ^ → 0 ∫ ∂ S A ⋅ d ℓ ∬ S d S = A ϕ ( r ) r sin θ d ϕ + A r ( ϕ + d ϕ ) d r − A ϕ ( r + d r ) ( r + d r ) sin θ d ϕ − A r ( ϕ ) d r d r r sin θ d ϕ = 1 r sin θ ∂ A r ∂ ϕ − 1 r ∂ ( r A ϕ ) ∂ r {\displaystyle {\begin{aligned}(\operatorname {curl} \mathbf {A} )_{\theta }=\lim _{S^{\perp {\boldsymbol {\hat {\theta }}}}\to 0}{\frac {\int _{\partial S}\mathbf {A} \cdot d\mathbf {\ell } }{\iint _{S}dS}}&={\frac {A_{\phi }(r)r\sin \theta \,d\phi +A_{r}(\phi +d\phi )\,dr-A_{\phi }(r+dr)(r+dr)\sin \theta \,d\phi -A_{r}(\phi )\,dr}{dr\,r\sin \theta \,d\phi }}\\&={\frac {1}{r\sin \theta }}{\frac {\partial A_{r}}{\partial \phi }}-{\frac {1}{r}}{\frac {\partial (rA_{\phi })}{\partial r}}\end{aligned}}}
( curl A ) ϕ = lim S ⊥ ϕ ^ → 0 ∫ ∂ S A ⋅ d ℓ ∬ S d S = A r ( θ ) d r + A θ ( r + d r ) ( r + d r ) d θ − A r ( θ + d θ ) d r − A θ ( r ) r d θ r d r d θ = 1 r ∂ ( r A θ ) ∂ r − 1 r ∂ A r ∂ θ {\displaystyle {\begin{aligned}(\operatorname {curl} \mathbf {A} )_{\phi }=\lim _{S^{\perp {\boldsymbol {\hat {\phi }}}}\to 0}{\frac {\int _{\partial S}\mathbf {A} \cdot d\mathbf {\ell } }{\iint _{S}dS}}&={\frac {A_{r}(\theta )\,dr+A_{\theta }(r+dr)(r+dr)\,d\theta -A_{r}(\theta +d\theta )\,dr-A_{\theta }(r)r\,d\theta }{r\,dr\,d\theta }}\\&={\frac {1}{r}}{\frac {\partial (rA_{\theta })}{\partial r}}-{\frac {1}{r}}{\frac {\partial A_{r}}{\partial \theta }}\end{aligned}}}
curl A = ( curl A ) r r ^ + ( curl A ) θ θ ^ + ( curl A ) ϕ ϕ ^ = 1 r sin θ ( ∂ ( A ϕ sin θ ) ∂ θ − ∂ A θ ∂ ϕ ) r ^ + 1 r ( 1 sin θ ∂ A r ∂ ϕ − ∂ ( r A ϕ ) ∂ r ) θ ^ + 1 r ( ∂ ( r A θ ) ∂ r − ∂ A r ∂ θ ) ϕ ^ {\displaystyle {\begin{aligned}\operatorname {curl} \mathbf {A} &=(\operatorname {curl} \mathbf {A} )_{r}\,{\hat {\boldsymbol {r}}}+(\operatorname {curl} \mathbf {A} )_{\theta }\,{\hat {\boldsymbol {\theta }}}+(\operatorname {curl} \mathbf {A} )_{\phi }\,{\hat {\boldsymbol {\phi }}}\\[1ex]&={\frac {1}{r\sin \theta }}\left({\frac {\partial (A_{\phi }\sin \theta )}{\partial \theta }}-{\frac {\partial A_{\theta }}{\partial \phi }}\right){\hat {\boldsymbol {r}}}+{\frac {1}{r}}\left({\frac {1}{\sin \theta }}{\frac {\partial A_{r}}{\partial \phi }}-{\frac {\partial (rA_{\phi })}{\partial r}}\right){\hat {\boldsymbol {\theta }}}+{\frac {1}{r}}\left({\frac {\partial (rA_{\theta })}{\partial r}}-{\frac {\partial A_{r}}{\partial \theta }}\right){\hat {\boldsymbol {\phi }}}\end{aligned}}}
The unit vector of a coordinate parameter u is defined in such a way that a small positive change in u causes the position vector r {\displaystyle \mathbf {r} } u {\displaystyle \mathbf {u} }
Therefore, ∂ r ∂ u = ∂ s ∂ u u {\displaystyle {\frac {\partial {\mathbf {r} }}{\partial u}}={\frac {\partial {s}}{\partial u}}\mathbf {u} } s is the arc length parameter.
For two sets of coordinate systems u i {\displaystyle u_{i}} v j {\displaystyle v_{j}} chain rule , d r = ∑ i ∂ r ∂ u i d u i = ∑ i ∂ s ∂ u i u ^ i d u i = ∑ j ∂ s ∂ v j v ^ j d v j = ∑ j ∂ s ∂ v j v ^ j ∑ i ∂ v j ∂ u i d u i = ∑ i ∑ j ∂ s ∂ v j ∂ v j ∂ u i v ^ j d u i . {\displaystyle d\mathbf {r} =\sum _{i}{\frac {\partial \mathbf {r} }{\partial u_{i}}}\,du_{i}=\sum _{i}{\frac {\partial s}{\partial u_{i}}}{\hat {\mathbf {u} }}_{i}du_{i}=\sum _{j}{\frac {\partial s}{\partial v_{j}}}{\hat {\mathbf {v} }}_{j}\,dv_{j}=\sum _{j}{\frac {\partial s}{\partial v_{j}}}{\hat {\mathbf {v} }}_{j}\sum _{i}{\frac {\partial v_{j}}{\partial u_{i}}}\,du_{i}=\sum _{i}\sum _{j}{\frac {\partial s}{\partial v_{j}}}{\frac {\partial v_{j}}{\partial u_{i}}}{\hat {\mathbf {v} }}_{j}\,du_{i}.}
Now, we isolate the i {\displaystyle i} th component. For i ≠ k {\displaystyle i{\neq }k} d u k = 0 {\displaystyle \mathrm {d} u_{k}=0} d u i {\displaystyle \mathrm {d} u_{i}} ∂ s ∂ u i u ^ i = ∑ j ∂ s ∂ v j ∂ v j ∂ u i v ^ j . {\displaystyle {\frac {\partial s}{\partial u_{i}}}{\hat {\mathbf {u} }}_{i}=\sum _{j}{\frac {\partial s}{\partial v_{j}}}{\frac {\partial v_{j}}{\partial u_{i}}}{\hat {\mathbf {v} }}_{j}.}
See also
References
External links ![{\displaystyle \theta \in [0,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c833964ea08aa30df8b6f56664461a5499b38144)
![{\displaystyle \varphi \in [0,2\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/adacea8b18fa91c9b01816ed054d2cf4f26b72fb)












![{\displaystyle \nabla ^{2}\left(\mathbf {P} \cdot \mathbf {Q} \right)=\mathbf {Q} \cdot \nabla ^{2}\mathbf {P} -\mathbf {P} \cdot \nabla ^{2}\mathbf {Q} +2\nabla \cdot \left[\left(\mathbf {P} \cdot \nabla \right)\mathbf {Q} +\mathbf {P} \times \nabla \times \mathbf {Q} \right]\quad }](https://wikimedia.org/api/rest_v1/media/math/render/svg/e39d7e00d51ce89633c61a8f5939819f39e8e8d8)






![{\displaystyle {\begin{aligned}(\operatorname {curl} \mathbf {A} )_{\rho }&=\lim _{S^{\perp {\hat {\boldsymbol {\rho }}}}\to 0}{\frac {\int _{\partial S}\mathbf {A} \cdot d{\boldsymbol {\ell }}}{\iint _{S}dS}}\\[1ex]&={\frac {A_{\phi }(z)\left(\rho +d\rho \right)\,d\phi -A_{\phi }(z+dz)\left(\rho +d\rho \right)\,d\phi +A_{z}(\phi +d\phi )\,dz-A_{z}(\phi )\,dz}{\left(\rho +d\rho \right)\,d\phi \,dz}}\\[1ex]&=-{\frac {\partial A_{\phi }}{\partial z}}+{\frac {1}{\rho }}{\frac {\partial A_{z}}{\partial \phi }}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8649ecbfebe77589420c030858b59022fe882071)

![{\displaystyle {\begin{aligned}(\operatorname {curl} \mathbf {A} )_{z}&=\lim _{S^{\perp {\hat {\boldsymbol {z}}}}\to 0}{\frac {\int _{\partial S}\mathbf {A} \cdot d\mathbf {\ell } }{\iint _{S}dS}}\\[1ex]&={\frac {A_{\rho }(\phi )\,d\rho -A_{\rho }(\phi +d\phi )\,d\rho +A_{\phi }(\rho +d\rho )(\rho +d\rho )\,d\phi -A_{\phi }(\rho )\rho \,d\phi }{\rho \,d\rho \,d\phi }}\\[1ex]&=-{\frac {1}{\rho }}{\frac {\partial A_{\rho }}{\partial \phi }}+{\frac {1}{\rho }}{\frac {\partial (\rho A_{\phi })}{\partial \rho }}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1728c015b8b117cd7a8229bb3735923203173ee)
![{\displaystyle {\begin{aligned}\operatorname {curl} \mathbf {A} &=(\operatorname {curl} \mathbf {A} )_{\rho }{\hat {\boldsymbol {\rho }}}+(\operatorname {curl} \mathbf {A} )_{\phi }{\hat {\boldsymbol {\phi }}}+(\operatorname {curl} \mathbf {A} )_{z}{\hat {\boldsymbol {z}}}\\[1ex]&=\left({\frac {1}{\rho }}{\frac {\partial A_{z}}{\partial \phi }}-{\frac {\partial A_{\phi }}{\partial z}}\right){\hat {\boldsymbol {\rho }}}+\left({\frac {\partial A_{\rho }}{\partial z}}-{\frac {\partial A_{z}}{\partial \rho }}\right){\hat {\boldsymbol {\phi }}}+{\frac {1}{\rho }}\left({\frac {\partial (\rho A_{\phi })}{\partial \rho }}-{\frac {\partial A_{\rho }}{\partial \phi }}\right){\hat {\boldsymbol {z}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/77b80d1002f75cfccc65fc1978533b2438fcd647)




![{\displaystyle {\begin{aligned}\operatorname {curl} \mathbf {A} &=(\operatorname {curl} \mathbf {A} )_{r}\,{\hat {\boldsymbol {r}}}+(\operatorname {curl} \mathbf {A} )_{\theta }\,{\hat {\boldsymbol {\theta }}}+(\operatorname {curl} \mathbf {A} )_{\phi }\,{\hat {\boldsymbol {\phi }}}\\[1ex]&={\frac {1}{r\sin \theta }}\left({\frac {\partial (A_{\phi }\sin \theta )}{\partial \theta }}-{\frac {\partial A_{\theta }}{\partial \phi }}\right){\hat {\boldsymbol {r}}}+{\frac {1}{r}}\left({\frac {1}{\sin \theta }}{\frac {\partial A_{r}}{\partial \phi }}-{\frac {\partial (rA_{\phi })}{\partial r}}\right){\hat {\boldsymbol {\theta }}}+{\frac {1}{r}}\left({\frac {\partial (rA_{\theta })}{\partial r}}-{\frac {\partial A_{r}}{\partial \theta }}\right){\hat {\boldsymbol {\phi }}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7d78f6369c32fc51bf5fa7d789aa7ded169e027)










