List of Mersenne primes and perfect numbers

Mersenne primes and perfect numbers are two deeply interlinked types of natural numbers in number theory. Mersenne primes, named after the friar Marin Mersenne, are prime numbers that can be expressed as 2^p − 1 for some positive integer p. For example, 3 is a Mersenne prime as it is a prime number and is expressible as 2² − 1. The exponents p corresponding to Mersenne primes must themselves be prime, although the vast majority of primes p do not lead to Mersenne primes—for example, 2¹¹ − 1 = 2047 = 23 × 89.

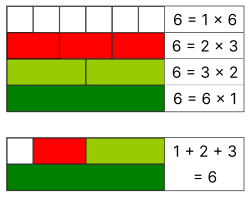
Perfect numbers are natural numbers that equal the sum of their positive proper divisors, which are divisors excluding the number itself. So, 6 is a perfect number because the proper divisors of 6 are 1, 2, and 3, and 1 + 2 + 3 = 6.

Euclid proved c. 300 BCE that every prime expressed as M_p = 2^p − 1 has a corresponding perfect number M_p × (M_p+1)/2 = 2^{p − 1} × (2^p − 1). For example, the Mersenne prime 2² − 1 = 3 leads to the corresponding perfect number 2^{2 − 1} × (2² − 1) = 2 × 3 = 6. In 1747, Leonhard Euler completed what is now called the Euclid–Euler theorem, showing that these are the only even perfect numbers. As a result, there is a one-to-one correspondence between Mersenne primes and even perfect numbers, so a list of one can be converted into a list of the other.

It is currently an open problem whether there are infinitely many Mersenne primes and even perfect numbers. The density of Mersenne primes is the subject of the Lenstra–Pomerance–Wagstaff conjecture, which states that the expected number of Mersenne primes less than some given x is (e^γ / log 2) × log log x, where e is Euler's number, γ is Euler's constant, and log is the natural logarithm. It is widely believed, but not proven, that no odd perfect numbers exist; numerous restrictive conditions have been proven, including a lower bound of 10¹⁵⁰⁰.

The following is a list of all 52 currently known (as of January 2025^[update]) Mersenne primes and corresponding perfect numbers, along with their exponents p. The largest 18 of these have been discovered by the distributed computing project Great Internet Mersenne Prime Search, or GIMPS; their discoverers are listed as "GIMPS / name", where the name is the person who supplied the computer that made the discovery. New Mersenne primes are found using the Lucas–Lehmer test (LLT), a primality test for Mersenne primes that is efficient for binary computers. Due to this efficiency, the largest known prime number has often been a Mersenne prime.

All possible exponents up to the 48th (p = 57,885,161) have been tested and verified by GIMPS as of October 2021^[update]. Ranks 49 and up are provisional, and may change in the unlikely event that additional primes are discovered between the currently listed ones. Later entries are extremely long, so only the first and last six digits of each number are shown, along with the number of decimal digits.

• OEIS sequence A000043 (Corresponding exponents p)
• OEIS sequence A000396 (Perfect numbers)
• OEIS sequence A000668 (Mersenne primes)
• List on GIMPS, with the full values of large numbers Archived 2020-06-07 at the Wayback Machine
• A technical report on the history of Mersenne numbers, by Guy Haworth Archived 2021-10-13 at the Wayback Machine