Parallel (operator)

The parallel operator (pronounced "parallel", following the parallel lines notation from geometry; also known as reduced sum, parallel sum or parallel addition) is a binary operation which is used as a shorthand in electrical engineering, but is also used in kinetics, fluid mechanics and financial mathematics. The name parallel comes from the use of the operator computing the combined resistance of resistors in parallel.
Overview
The parallel operator represents the reciprocal value of a sum of reciprocal values (sometimes also referred to as the "reciprocal formula" or "harmonic sum") and is defined by:
where a, b, and are elements of the extended complex numbers
The operator gives half of the harmonic mean of two numbers a and b.
As a special case, for any number :
Further, for all distinct numbers :
with representing the absolute value of , and meaning the minimum (least element) among x and y.
If and are distinct positive real numbers then
The concept has been extended from a scalar operation to matrices and further generalized.
Notation
The operator was originally introduced as reduced sum by Sundaram Seshu in 1956, studied as operator ∗ by Kent E. Erickson in 1959, and popularized by Richard James Duffin and William Niles Anderson, Jr. as parallel addition or parallel sum operator : in mathematics and network theory since 1966. While some authors continue to use this symbol up to the present, for example, Sujit Kumar Mitra used ∙ as a symbol in 1970. In applied electronics, a ∥ sign became more common as the operator's symbol around 1974. This was often written as doubled vertical line (||) available in most character sets (sometimes italicized as //), but now can be represented using Unicode character U+2225 ( ∥ ) for "parallel to". In LaTeX and related markup languages, the macros \| and \parallel are often used (and rarely \smallparallel is used) to denote the operator's symbol.
Properties
Let represent the extended complex plane excluding zero, and the bijective function from to such that One has identities
and
This implies immediately that is a field where the parallel operator takes the place of the addition, and that this field is isomorphic to
The following properties may be obtained by translating through the corresponding properties of the complex numbers.
Field properties
As for any field, satisfies a variety of basic identities.
It is commutative under parallel and multiplication:
It is associative under parallel and multiplication:
Both operations have an identity element; for parallel the identity is while for multiplication the identity is 1:
Every element of has an inverse under parallel, equal to the additive inverse under addition. (But 0 has no inverse under parallel.)
The identity element is its own inverse,
Every element of has a multiplicative inverse :
Multiplication is distributive over parallel:
Repeated parallel
Repeated parallel is equivalent to division,
Or, multiplying both sides by n,
Unlike for repeated addition, this does not commute:
Binomial expansion
Using the distributive property twice, the product of two parallel binomials can be expanded as
The square of a binomial is
The cube of a binomial is
In general, the nth power of a binomial can be expanded using binomial coefficients which are the reciprocal of those under addition, resulting in an analog of the binomial formula:
Logarithm and exponential
The following identities hold:
Factoring parallel polynomials
As with a polynomial under addition, a parallel polynomial with coefficients in (with ) can be factored into a product of monomials:
for some roots (possibly repeated) in
Analogous to polynomials under addition, the polynomial equation
implies that for some k.
Quadratic formula
A linear equation can be easily solved via the parallel inverse:
To solve a parallel quadratic equation, complete the square to obtain an analog of the quadratic formula
Including zero
The extended complex numbers including zero, is no longer a field under parallel and multiplication, because 0 has no inverse under parallel. (This is analogous to the way is not a field because has no additive inverse.)
For every non-zero a,
The quantity can either be left undefined (see indeterminate form) or defined to equal 0.
Precedence
In the absence of parentheses, the parallel operator is defined as taking precedence over addition or subtraction, similar to multiplication.
Applications
There are applications of the parallel operator in mechanics, electronics, optics, and study of periodicity:
Reduced mass
Given masses m and M, the reduced mass is frequently applied in mechanics. For instance, when the masses orbit each other, the moment of inertia is their reduced mass times the distance between them.
Circuit analysis
In electrical engineering, the parallel operator can be used to calculate the total impedance of various serial and parallel electrical circuits. There is a duality between the usual (series) sum and the parallel sum.
For instance, the total resistance of resistors connected in parallel is the reciprocal of the sum of the reciprocals of the individual resistors.
Likewise for the total capacitance of serial capacitors.
Coalescence of independent probability density functions.
The coalesced density function fcoalesced(x) of n independent probability density functions f1(x), f2(x), …, fn(x), is equal to the reciprocal of the sum of the reciprocal densities.
Lens equation
In geometric optics the thin lens approximation to the lens maker's equation.
Synodic period
The time between conjunctions of two orbiting bodies is called the synodic period. If the period of the slower body is T2, and the period of the faster is T1, then the synodic period is
Examples
Question:
- Three resistors , and are connected in parallel. What is their resulting resistance?
Answer:
- The effectively resulting resistance is ca. 57 kΩ.
Question:
- A construction worker raises a wall in 5 hours. Another worker would need 7 hours for the same work. How long does it take to build the wall if both workers work in parallel?
Answer:
- They will finish in close to 3 hours.
Implementation

Suggested already by Kent E. Erickson as a subroutine in digital computers in 1959, the parallel operator is implemented as a keyboard operator on the Reverse Polish Notation (RPN) scientific calculators WP 34S since 2008 as well as on the WP 34C and WP 43S since 2015, allowing to solve even cascaded problems with few keystrokes like270↵ Enter180∥120∥.
Projective view
Given a field F there are two embeddings of F into the projective line P(F): z → [z : 1] and z → [1 : z]. These embeddings overlap except for [0:1] and [1:0]. The parallel operator relates the addition operation between the embeddings. In fact, the homographies on the projective line are represented by 2 x 2 matrices M(2,F), and the field operations (+ and ×) are extended to homographies. Each embedding has its addition a + b represented by the following matrix multiplications in M(2,A):
The two matrix products show that there are two subgroups of M(2,F) isomorphic to (F,+), the additive group of F. Depending on which embedding is used, one operation is +, the other is
Notes
References
Further reading
- Pekarev, Èdward L.; Šmul'jan, Ju. L. (1976-04-30). "Parallel Addition and Parallel Subtraction of Operators". Mathematics of the USSR-Izvestiya. 10 (2). American Mathematical Society: 351–370. Bibcode:1976IzMat..10..351P. doi:10.1070/IM1976v010n02ABEH001694.
- Duffin, Richard James; Morley, Tom D. (July 1978). "Almost Definite Operators and Electro-mechanical Systems". SIAM Journal on Applied Mathematics. 35 (1). Society for Industrial and Applied Mathematics (SIAM): 21–30. doi:10.1137/0135003. JSTOR 2101028. (10 pages)
- Morley, Tom D. (July 1979). "Parallel Summation, Maxwell's Principle and the Infimum of Projections" (PDF). Journal of Mathematical Analysis and Applications. 70 (1). Department of Mathematics, University of Illinois at Urbana-Champaign, Urbana, Illinois, USA: 33–41. doi:10.1016/0022-247X(79)90073-8. Archived from the original on 2020-08-20. Retrieved 2020-08-20.
- Seeger, Alberto (May 1990) [1988-03-22]. "Direct and Inverse Addition in Convex Analysis and Applications" (PDF). Journal of Mathematical Analysis and Applications. 148 (2). Department of Mathematics, University of Washington, Seattle, Washington, USA: Academic Press, Inc.: 317–349. doi:10.1016/0022-247X(90)90004-Y. Archived (PDF) from the original on 2020-08-20. Retrieved 2020-08-20. (33 pages)
- Bryant, Randal E.; Tygar, J. Doug; Huang, Lawrence P. (1994). "Geometric characterization of series-parallel variable resistor networks" (PDF). IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications. 41 (11): 686–698. doi:10.1109/81.331520. Archived from the original (PDF) on 2017-08-14.
- Antezana, Jorge; Corach, Gustavo; Stojanoff, Demetrio (April 2006) [2005-09-14]. "Bilateral Shorted Operators and Parallel Sums" (PDF). Linear Algebra and Its Applications. 414 (2–3). La Plata, Argentina & Buenos Aires, Argentina: 570–588. arXiv:math/0509327. doi:10.1016/j.laa.2005.10.039. Archived (PDF) from the original on 2017-08-09. Retrieved 2020-08-20. [14] (19 pages)
- Chansangiam, Pattrawut (February 2016) [August 2015, July 2015]. "Mathematical aspects for electrical network connections". KKU Engineering Journal. 43 (1): 47–54. doi:10.14456/kkuenj.2016.8. Archived (PDF) from the original on 2020-08-20. Retrieved 2020-08-20.
- Besenyei, Ádám (2016-09-01). "The irresistible inequality of Milne" (PDF). Budapest: Department of Applied Analysis and Computational Mathematics, Eötvös Loránd University. CIA2016. Archived (PDF) from the original on 2019-08-08. Retrieved 2019-08-11.
- "7.5 Electrical Characteristics: VCC = 5 V / 7.6 Electrical Characteristics: VCC = 2.7 V / 9.1.2.1 Inverting Comparator with Hysteresis". TLV3201, TLV3202: TLV320x 40-ns, microPOWER, Push-Pull Output Comparators (PDF). Revision B. Dallas, Texas, USA: Texas Instruments Incorporated. 2022-06-03 [2016, 2012]. pp. 5, 6, 13–14 [13]. SBOS561B. Archived (PDF) from the original on 2022-08-17. Retrieved 2022-08-18. p. 5:
PARAMETER […] TYP […] UNIT […] INPUT IMPEDANCE […] Common mode […] 1013 ∥ 2 […] Ω ∥ pF […] Differential […] 1013 ∥ 4 […] Ω ∥ pF […]
(37 pages) (NB. Unusual usage of ∥ for both values and units.)























![{\displaystyle {\begin{aligned}a\parallel b&=b\parallel a\\[3mu]ab&=ba\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33fdcf548e5e335be871903cc2d0cc02147439db)













![{\displaystyle {\begin{aligned}(a\parallel b)(c\parallel d)&=a(c\parallel d)\parallel b(c\parallel d)\\[3mu]&=ac\parallel ad\parallel bc\parallel bd.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75796fff00982215ddf28125ac13967f56303ac6)
![{\displaystyle {\begin{aligned}(a\parallel b)^{2}&=a^{2}\parallel ab\parallel ba\parallel b^{2}\\[3mu]&=a^{2}\parallel {\tfrac {1}{2}}ab\parallel b^{2}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5cc365e2090c31a9a827d434b9def70074105726)












![{\displaystyle {\begin{aligned}ax\parallel b&=\infty \\[3mu]\implies x&=-{\frac {b}{a}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f17b63944689d920e5fe583a2faa06bad488bc9)
![{\displaystyle {\begin{aligned}ax^{2}\parallel bx\parallel c&=\infty \\[5mu]x^{2}\parallel {\frac {b}{a}}x&=-{\frac {c}{a}}\\[5mu]x^{2}\parallel {\frac {b}{a}}x\parallel {\frac {4b^{2}}{a^{2}}}&=\left(-{\frac {c}{a}}\right)\parallel {\frac {4b^{2}}{a^{2}}}\\[5mu]\left(x\parallel {\frac {2b}{a}}\right)^{2}&={\frac {b^{2}\parallel -{\tfrac {1}{4}}ac}{{\tfrac {1}{4}}a^{2}}}\\[5mu]\implies x&={\frac {(-b)\parallel \pm {\sqrt {b^{2}\parallel -{\tfrac {1}{4}}ac}}}{{\tfrac {1}{2}}a}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/499ed1736b0e0cf7cea1e6de3291ffaacb848cfe)





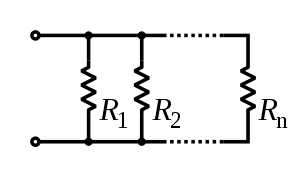
![{\displaystyle {\begin{aligned}{\frac {1}{R_{\text{eq}}}}&={\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}+\cdots +{\frac {1}{R_{n}}}\\[5mu]R_{\text{eq}}&=R_{1}\parallel R_{2}\parallel \cdots \parallel R_{n}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92fddb4b991c03b156b12dd85c3cca8c3a3f66c1)
![{\displaystyle {\begin{aligned}{\frac {1}{f_{coalesced}(x)}}&={\frac {1}{f_{1}(x)}}+{\frac {1}{f_{2}(x)}}+\cdots +{\frac {1}{f_{n}(x)}}\\[5mu]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/18c48675447b99b2224567d3f635528614d9efa5)





![{\displaystyle {\begin{aligned}R_{1}\parallel R_{2}\parallel R_{3}&=270\,\mathrm {k\Omega } \parallel 180\,\mathrm {k\Omega } \parallel 120\,\mathrm {k\Omega } \\[5mu]&={\frac {1}{{\dfrac {1}{270\,\mathrm {k\Omega } }}+{\dfrac {1}{180\,\mathrm {k\Omega } }}+{\dfrac {1}{120\,\mathrm {k\Omega } }}}}\\[5mu]&\approx 56.84\,\mathrm {k\Omega } \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8635ca3fd9bb42d8a264124fe968db472bb0486d)

![{\displaystyle {\begin{aligned}{\begin{pmatrix}1&0\\a&1\end{pmatrix}}{\begin{pmatrix}1&0\\b&1\end{pmatrix}}&={\begin{pmatrix}1&0\\a+b&1\end{pmatrix}},\\[10mu]{\begin{pmatrix}1&a\\0&1\end{pmatrix}}{\begin{pmatrix}1&b\\0&1\end{pmatrix}}&={\begin{pmatrix}1&a+b\\0&1\end{pmatrix}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a775bf62a63081caef53f3f33667ce290bbc4f5)
