Portal:Mathematics

Portal topics: Activities; Culture; Geography; Health; History; Mathematics; Nature; People; Philosophy; Religion; Society; Technology; Random portal

The Mathematics Portal

Mathematics is the study of numbers, quantity, space, pattern, structure, and change. Mathematics is used throughout the world as an essential tool in many fields, including natural science, engineering, medicine, and the social sciences. It is used for calculation and considered as the most important subject. Applied mathematics, the branch of mathematics concerned with application of mathematical knowledge to other fields, inspires and makes use of new mathematical discoveries and sometimes leads to the development of entirely new mathematical disciplines, such as statistics and game theory. Mathematicians also engage in pure mathematics, or mathematics for its own sake, without having any application in mind. There is no clear line separating pure and applied mathematics, and practical applications for what began as pure mathematics are often discovered. (Full article...)

Refresh with new selections below (purge)

edit

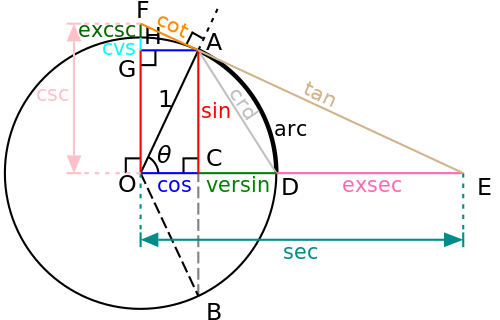
Selected article – show another

The continuum hypothesis is a hypothesis, advanced by Georg Cantor, about the possible sizes of infinite sets. Cantor introduced the concept of cardinality to compare the sizes of infinite sets, and he showed that the set of integers is strictly smaller than the set of real numbers. The continuum hypothesis states the following:

There is no set whose size is strictly between that of the integers and that of the real numbers.

Or mathematically speaking, noting that the cardinality for the integers $|\mathbb {Z} |$ is $\aleph _{0}$ ("aleph-null") and the cardinality of the real numbers $|\mathbb {R} |$ is $2^{\aleph _{0}}$ , the continuum hypothesis says

\nexists \mathbb {A} :\aleph _{0}<|\mathbb {A} |<2^{\aleph _{0}}.

This is equivalent to:

2^{\aleph _{0}}=\aleph _{1}

The real numbers have also been called the continuum, hence the name. (Full article...)

View all selected articles

edit

Selected image – show another

animation of patterns of black pixels moving on a white background

Conway's Game of Life

Credit: User:Protious (animation) & Hyperdeath (original still image)

Conway's Game of Life is a cellular automaton devised by the British mathematician John Horton Conway in 1970. It is an example of a zero-player game, meaning that its evolution is completely determined by its initial state, requiring no further input as the game progresses. After an initial pattern of filled-in squares ("live cells") is set up in a two-dimensional grid, the fate of each cell (including empty, or "dead", ones) is determined at each step of the game by considering its interaction with its eight nearest neighbors (the cells that are horizontally, vertically, or diagonally adjacent to it) according to the following rules: (1) any live cell with fewer than two live neighbors dies, as if caused by under-population; (2) any live cell with two or three live neighbors lives on to the next generation; (3) any live cell with more than three live neighbors dies, as if by overcrowding; (4) any dead cell with exactly three live neighbors becomes a live cell, as if by reproduction. By repeatedly applying these simple rules, extremely complex patterns can emerge. In this animation, a breeder (in this instance called a puffer train, colored red in the final frame of the animation) leaves guns (green) in its wake, which in turn "fire out" gliders (blue). Many more complex patterns are possible. Conway developed his rules as a simplified model of a hypothetical machine that could build copies of itself, a more complicated version of which was discovered by John von Neumann in the 1940s. Variations on the Game of Life use different rules for cell birth and death, use more than two states (resulting in evolving multicolored patterns), or are played on a different type of grid (e.g., a hexagonal grid or a three-dimensional one). After making its first public appearance in the October 1970 issue of Scientific American, the Game of Life popularized a whole new field of mathematical research called cellular automata, which has been applied to problems in cryptography and error-correction coding, and has even been suggested as the basis for new discrete models of the universe.

More selected pictures

edit

Did you know – view different entries

... if the integer n is prime, then the nth Perrin number is divisible by n?
...that it is impossible to trisect a general angle using only a ruler and a compass?
...that in a group of 23 people, there is a more than 50% chance that two people share a birthday?
...that the 1966 publication disproving Euler's sum of powers conjecture, proposed nearly 200 years earlier, consisted of only two sentences?
...the hyperbolic trigonometric functions of the natural logarithm can be represented by rational algebraic fractions?
... that economists blame market failures on non-convexity?
... that, according to the pizza theorem, a circular pizza that is sliced off-center into eight equal-angled wedges can still be divided equally between two people?